The effect of multi-part payments on the Balance Disovery Attack

My PhD research is mainly on the Balance Discovery Attack (BDA). The BDA was introduced (in academia) by Herrera-Joancomartí et al.. In their paper they used the term balance discovery attack and balance disclosure attack interchangeably. Nowadays the term probing or probing attack is more commonly used, but I prefer BDA, so I'll keep using that while shouting at the clouds.

The BDA is an attack on privacy. It can be used to discover balances of payment channels, but when used over a longer period of time it can also be used to detect actual payments. These are things we want to keep private, so it is interesting to look at ways of preventing this data from being leaked. Multi-part payments, and more specifically Payments Split & Switch (PSS) has some surprising effects that can prevent data from being leaked in ways that I will try to explain in this post.

The Balance Discovery Attack

As I explained in my post on payments in Lightning Network, it is the sender who determines the route to the receiver. Because the sender does not know the balances of the route it selected, it can inadvertently select a route that has a payment channel in it with not enough liquidity to relay the payment. The relaying node will signal this by returning an InsufficientFunds or TemporaryChannelFailure error. If the sender succeeds in finding a route with enough liquidity, the payment goes through. But what if the sender uses a random payment hash, not used by any invoice? In that case if the sender finds a route with enough liquidity, the receiver returns with an UnknownPaymentHash error. This is the trick of the BDA: By using a random payment hash, the sender can distinguish between enough liquidity and insufficient liquidity without having to make a payment that actually succeeds.

By continuously probing the exact same route with different amounts and by choosing those amounts wisely i.e. via a binary search algorithm, the attacker can determine the exact balance of a payment channel with a precision of up to one millisatoshi.

Source-based routing

If the the sender in LN wasn't the one who determined the route, (and didn't knew exactly through which channels a payment travels) the BDA wouldn't be possible. But LN uses source-based routing, and the network acts like an old-fashioned circuit-switched network, and so the BDA is possible. LN works like this because of privacy. The sender doesn't want to divulge the receiver, so it can't include the receiver in the header of a "payment package" like would be the case in a packet-switched network. Privacy, as always, is a trade-off and in this case the requirement of keeping the receiver hidden opens LN up for the BDA, which leaks information about the amount paid.

Parallel Channels

But there's a case where the sender doesn't exactly knows which channel a payment takes. This is the case where a payment traverses between two nodes that have multiple channels between them. Nodes open new channels between them e.g. if a channel is depleted on one side. The node on that side wants to send payments while keeping the ability to receive payments through the depleted channel, so it opens a new channel.

When two nodes having a hop between them with multiple channels receive a request for relaying a payment, they are free to choose either channel between them to forward the payment, as long as the balance allows for it. Earlier work on BDAs didn't appreciate this fact, but Alex Biryukov et al. wrote a great paper exploring the effects of parallel channels on BDAs, and showed that parallel channels decrease the amount of information that can be obtained by an attacker mounting a BDA.

Link MPP, PSS and BDA

Although an attacker can't be certain which channel is used in a hop with parallel channels (and I'm glossing over some details here), in Alex's model the attacker still assumes that a payment goes through one single channel. But if a hop would use Link MPP or better yet PSS, an attacker couldn't even make that assumption. The relaying node is free to split up the payment as it sees fit, and the next node reassembles the parts and forwards the payment. (For more info on multi-part payments like Link MPP and PSS, please read my post explaining all MPPs)

If the assumption that a payment travels through a single channel can't be made, life becomes a lot harder for the attacker. Because interpreting the results from a BDA becomes a problem of solving a system of mutiple linear inequalities. To explain, I first need to introduce Alex Biryukov's generalized geometrical model.

Generalized Geometrical Model

The geometrical model is a model where all parallel channels in a hop are represented by a (hyper-)rectangle. Each dimension of this object represents a single channel. So a hop with just a single channel is represented by a line from zero to the capacity of the channel, a hop with two parallel channels is represented by a rectangle with one vertex at the origin and the opposit vertex at the point that lies at the coordinate of of the capacities of both channels, a hop with three parallel channels is represented by a cube and so on. Let's take a hop with two channels as an example and imagine the rectangle that represents it. Each point inside the rectangle is a possible combination of the two balances.

For now, let's assume payments go through single channels (no MPP yet). A probe gives us information with which we can adapt our geometrical object. A succesful probe means that the balances of both channels can't both be lower than the probing amount. So we can cut away a square from our rectangle that has sides equal to the probing amount. Depending on the probing direction, that square has its lower left vertex at the origin, or its upper right vertex at the upper right vertex of our rectangle. However, if the probe failed we know for sure that both balances are inadequate for relaying the probe. So instead of cutting the square away, we now know for sure that the balances of both channels lie with that square. So probing parallel channels becomes a game of chipping away squares, or chipping away everything outside the square, from the original rectangle.

After a full BDA of parallel channels, you don't necessarily get the exact balance, but you get a small set of possible balances. The set being smaller if the dimensions (the number of parallel channels) are lower.

The Geometrical Model with PSS

But when we introduce PSS into the mix, things start to get interesting. Not only does PSS allow for alternative routes (that introduce extra hops), it also allows for payment splitting over different hops. And all this without the sender knowing any of it. So from the perspective of the attacker in a BDA, a lot of uncertainty is introduced. Firstly, although the attacker is still the one who creates the route (it's still source-based routing after all), the attacker does need to consider alternative routes from one node to the next for each hop in the route. Secondly, the attacker needs to consider every possible split of payment over the possible routes from one hop to the next.

We can still capture this in a geometrical model. Again we start with a (hyper-)rectangle. But instead of the parallel channels in a hop, we need to consider all routes possible routes from one node to the next. But here the attacker has to make an assumption, with regards to the length of the routes it is willing to consider. In my research I made the assumption that PSS was only feasible over alternative routes with one intermediary hop. Every possible route from one hop to the next is now a dimension of our (hyper-)rectangle. This includes all parallel channels if there are any, but now also alternative routes with a single intermediary hop.

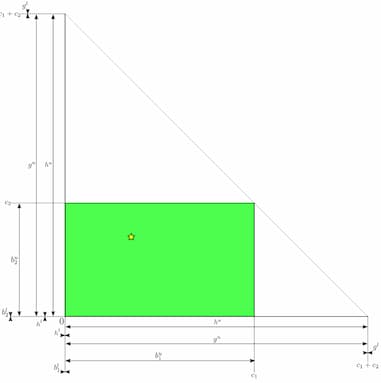
The attacker also needs to change it interpretation of the probing results. A sucessful probe is still grounds for adjusting the lower bounds, but before we could cut away a rectangle (the balances of both channels can't both be lower than the probing amount). But with PSS it's different. A succesful probe in PSS means that the balances of both channels can't together be lower than the probing amount. Geometrically this means we can cut away a triangle containing all points in our (hyper-)rectangle that together are less than the probing amount. A failed probe indicates an upper bound where we can cut away all points that together are more than the probing amount.

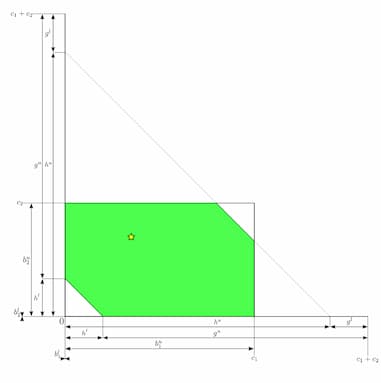
So instead of chipping away squares we are now chipping away triangles that are half the size of those squares. A BDA still reduces the set of possible balances quite drastically, but it does it less than without the assumption of PSS. In other words, a (hyper-)rectangle with the same amount of dimensions and the same size is reduced to a bigger set with the assumption of PSS. Moreover, the (hyper-)rectangle have more dimensions to begin with because of the alternative routes that need to be considered, making the resulting set of possible balances even bigger than that set in the same setting but without PSS.

Computational Cost

So PSS makes BDA less effective, but also computationally more expensive. The old BDA algorithms are pretty much just binary searches with a time complexity of \(O(\log n)\). But with PSS the counting the coordinates (or lattice points as the cool kids call them) in that (hyper-)rectangle while chipping away (hyper-)triangles becomes increasingly complex, and the main bottle neck for the whole BDA algorithm.

We can describe the (hyper-)rectangle with the cut-away triangles as a system of mutiple linear inequalities. For each dimension (let's say a 3-dimensional cube with dimensions x,y and z) we can describe the cube itself with six inequalities:

\[ \begin{align} x & > -1 \\ x & \leq c_x \\ y & > -1 \\ y & \leq c_y \\ z &> -1 \\ z & \leq c_z \\ \end{align} \]

Where \(c_x, c_y, c_z\) are the capacities of the channels represented by that dimension. Given a succesful probe and a failed probe for the amounts \(a_s\) and \(a_f\), we can add two inequalities:

\[ \begin{align} x + y + z & > a_s \\ x + y + z & \leq a_f \\ \end{align} \]

The set of points that satisfy all inequalities is the set of possible balances. Finding this set is a problem of counting lattice points in a convex polytope. A polytope is a fancy word for objects with flat sides. Convex means it doesn't curve inwards on itself: the shape doesn't have any "dents". Barvinok created an algorithm for counting points in such shapes that runs in polynomial time. So now our BDA algorithm bumps up from \(O(\log n)\) to \(O(n^{c})\) just because of the counting of the points in our weird hypershape.

Summary

So that's the bottomline: PSS makes BDA less effective (the resulting set of possible balances is bigger than before) and computationally way more complex.

If you got this far, maybe you would also like to get really deep into the weeds and read my preprint on exactly this topic. You can find it at the Cryptology ePrint Archive